- سوالات استخدامی نقاشی ایرانی از دیروز تا امروز (دبیر فرهنگ و هنر)
- سوالات استخدامی هنر و تمدن اسلامی (دبیر فرهنگ و هنر)
- سوالات استخدامی دبیری فرهنگ و هنر با پاسخنامه (حیطه تخصصی)
- تولید صابون از پلاستیک های دور ریز
- پنج توصیه ویژه برای والدینی که فرزندشان کنکوری است
- مهروماه در سی و پنجمین نمایشگاه کتاب تهران
- سوالات ضمن خدمت محور مهارت های فردی و اجتماعی ( زندگی با قرآن و عترت و آشنایی با حکمت های نهج البلاغه ) سال ۱۴۰۳
- پاورپوینت گل های آپارتمانی
- پاورپوینت گل های آپارتمانی زینتی
- سوالات استخدامی راهنمای معلم فرهنگ و هنر (دبیر فرهنگ و هنر)
آخرین مطالب
امکانات وب
محیط بیضی، اندازه منحنی بسته تشکیلدهنده آن را نمایش میدهد. با وجود فرمولهای تقریبی متعدد، تا کنون هیچ رابطه دقیقی برای محاسبه این اندازه ارائه نشده است. تمام فرمولهای تقریبی، با مقداری خطا همراه هستند. با این حال، برخی از آنها، اندازه محیط بیضی را با دقت بسیار خوبی محاسبه میکنند در این مقاله، به معرفی 10 فرمول برای محاسبه محیط بیضی میپردازیم. این فرمولها بر اساس روابط تقریبی، سریهای بینهایت و انتگرال نوشته میشوند.
فیلم آموزشی محیط بیضی
محیط بیضی چیست؟
محیط بیضی، طول منحنی بستهای است که محدوده اطراف این شکل را مشخص میکند. در تصویر زیر، نقطه برخورد خطهای آبی و قرمز، در حال حرکت بر روی محیط بیضی است. برخلاف بسیاری از شکلهای هندسی، هیچ فرمول مشخصی برای محاسبه دقیق محیط بیضی وجود ندارد.
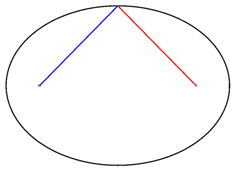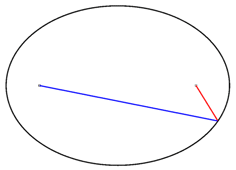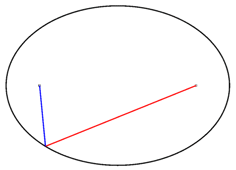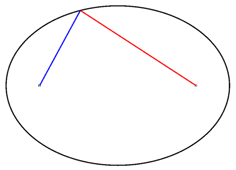
در هر بیضی، مجموع فاصله نقاط روی محیط تا کانونها (مجموع خطهای آبی و قرمز در تصویر بالا)، همواره یک عدد ثابت است.
محیط بیضی چگونه بدست می آید ؟
محیط بیضی، با استفاده از تقریبهای ریاضی و اندازه شعاعهای بیضی به دست میآید. تا کنون، چندین فرمول ریاضی برای محاسبه محیط بیضی ارائه شدهاند. متاسفانه هیچ یک از این فرمولها نمیتوانند اندازه دقیق محیط را تعیین کنند. تصویر زیر، شعاعهای بزرگ و کوچک بیضی را نمایش میدهد.
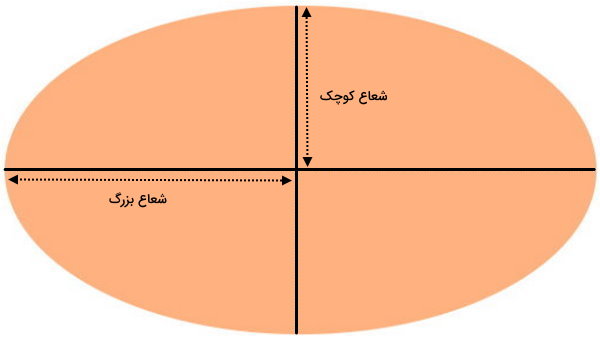
شعاع بزرگ، فاصله بین گوشه محور اصلی تا مرکز بیضی و شعاع کوچک، فاصله بین گوشه محور فرعی تا مرکز بیضی است. شعاعها، علاوه بر تعیین محیط، در محاسبه مساحت بیضی نیز به کار برده میشوند. در بخشهای بعدی، انواع فرمولهای تعیین محیط بیضی را به ترتیب سادگی و میزان خطا معرفی خواهیم کرد.
محاسبه محیط بیضی با فرمول های تقریبی
پنج فرمول تقریبی متداول برای محاسبه محیط حالتهای مختلف بیضی وجود دارند. در ادامه، این تقریبها را بر اساس دقت و کاربرد مورد بررسی قرار میدهیم.
فرمول اول: تقریب محیط بیضی از روی محیط دایره
سادهترین فرمول تقریبی محاسبه محیط بیضی، به صورت زیر نوشته میشود:
$$
P approx pi (a + b)
$$
- P: محیط بیضی
- a: شعاع بزرگ بیضی
- b: شعاع کوچک بیضی
در حالت کلی، خطای رابطه بالا، بسیار بیشتر از دیگر روابط تقریبی است. با این وجود، این رابطه، محیط یکی از حالتهای خاص بیضی را به طور دقیق محاسبه میکند. پیش از اینکه به معرفی فرمولهای دقیقتر محیط بیضی بپردازیم، این حالت خاص را مورد بررسی قرار میدهیم. دایره، حالت خاصی از یک بیضی است که شعاعهای برابر دارد. بررسی محیط دایره میتواند درک خوبی را از نحوه محاسبه محیط بیضی فراهم کند. فرمول محیط دایره به صورت زیر نوشته میشود:
$$
C = pi d
$$
- C: محیط دایره
- d: قطر دایره
قطر دایره، دو برابر شعاع آن (۲r) است. بنابراین میتوانیم فرمول محیط دایره را به صورت زیر بنویسیم:
$$
C = pi ( ۲ r )
$$
یا
$$
C = pi ( r + r )
$$
اگر اندازههای شعاع بزرگ و کوچک بیضی برابر باشند، فرمول محیط آن به شکل زیر در میآید:
$$
C = pi ( a + a )
$$
این فرمول، همان فرمول محیط دایره است. در صورت وجود اختلاف بین اندازه شعاعهای کوچک و بزرگ، رابطه بالا با خطا همراه میشود. این خطا میتواند به بالای 10 درصد نیز برسد. البته اگر اختلاف اندازه بین شعاعها کم یا ناچیز باشد، استفاده از فرمول اول، نتایج قابل قبولی را ارائه میکند.
مثال 1: محاسبه محیط بیضی و خطای آن
دو بیضی با اطلاعات زیر را در نظر بگیرید:
- بیضی 1
- شعاع بزرگ: 4
- شعاع کوچک: 1
- بیضی 2
- شعاع بزرگ: 2
- شعاع کوچک: 1
بر اساس یکی از دقیقترین روشهای محاسبه، محیط بیضی 1 برابر با 17/16 و محیط بیضی 2 برابر با 9/69 شده است. با استفاده از تقریب محیط بیضی با فرمول محیط دایره، به سوالات زیر پاسخ دهید:
- محیط هر یک از بیضیها چقدر است؟
- اختلاف محاسباتی محیط نسبت به روش دقیقتر چقدر است؟
- اختلاف محاسبات برای کدام بیضی کمتر است و دلیل آن چیست؟
به منظور محاسبه محیط هر یک از بیضیها از فرمول زیر استفاده میکنیم:
$$
P approx pi (a + b)
$$
- P: محیط بیضی
- a: شعاع بزرگ
- b: شعاع کوچک
محیط اولین بیضی برابر است با:
$$
P_۱ approx pi ( a_۱ + b_۱ )
$$
$$
P_۱ approx ۳/۱۴ times ( ۴ + ۱ )
$$
$$
P_۱ approx ۳/۱۴ times ( ۵ )
$$
$$
P_۱ approx ۱۵/۷
$$
محیط دومین بیضی از رابطه زیر به دست میآید:
$$
P_۲ approx pi (a_۲ + b_۲)
$$
$$
P_۲ approx ۳/۱۴ times (۲ + ۱)
$$
$$
P_۲ approx ۳/۱۴ times (۳)
$$
$$
P_۲ approx ۹/۴۲
$$
اختلاف محاسبات بیضی 1 برابر است با:
$$
E_۱ = ۱۷/۱۶ – ۱۵/۷ = ۱/۶۴
$$
این اختلاف، خطایی حدود 10 درصد را نمایش میدهد. اختلاف محاسبات برای بیضی 2 نیز به صورت زیر محاسبه میشود:
$$
E_۲ = ۹/۶۹ – ۹/۴۲ = ۰/۲۷
$$
این اختلاف، خطایی حدود 3 درصد را نمایش میدهد. همانطور که مشاهده میکنید، خطای محاسبات برای بیضی 2 کمتر است. فرمول استفاده شده در این مثال، برای تعیین محیط بیضیهای شبیه به دایره کاربرد دارد. اختلاف اندازه شعاعهای بیضی ۲، نسبت به اختلاف اندازه شعاعهای بیضی 1 کمتر بوده و شکل آن به دایره شبیهتر بود. به همین دلیل، محاسبه محیط بیضی 2، خطای کمتری داشت.
فرمول دوم
اگر اختلاف اندازه بین شعاعهای بیضی قابل توجه باشد، از فرمول تقریبی زیر برای محاسبه محیط استفاده میشود:
$$
P approx pi sqrt{ ۲ left( a^{ ۲ } + b^{ ۲ }right)}
$$
فرمول سوم
فرمول زیر، یکی دیگر از تقریبهای پرکاربرد برای محاسبه محیط بیضی را نمایش میدهد:
$$
P approx pileft[ frac{ ۳ }{ ۲ }( a+b )-sqrt{ a b}right]
$$
این تقریب نیز مانند تقریب دوم، در هنگام وجود اختلاف زیاد بین اندازه شعاعهای بیضی به کار میرود. با این وجود، مقدار به دست آمده از فرمول سوم، کمتر از فرمول دوم است. بنابراین، میانگین این دو تقریب میتواند به محیط واقعی نزدیکتر باشد.
فرمول چهارم و پنجم: تقریب های رامانوجان
سرینیواسا رامانوجان، یکی از ریاضیدانان برجسته دنیا، دو فرمول برای محاسبه محیط بیضی ارائه کرده است. با وجود سادگی و کاربری آسان، این فرمولها نسبت به فرمولهای قبلی، از دقت بیشتری بهره میبرند. عبارت جبری اولین تقریب رامانوجان به صورت زیر نوشته میشود:
$$
P approx pi[ ۳ ( a + b ) – sqrt{( ۳ a + b )( a + ۳ b)}]
$$
تقریب دوم رامانوجان نیز عبارت است از:
$$
P approx pi( a + b )left( 1 + frac{ ۳ h }{ ۱۰ + sqrt{ ۴ – ۳ h }}right)
$$
h، ثابتی است که از رابطه زیر محاسبه میشود:
$$
h = frac{( a – b )^{ ۲ }}{( a + b )^{ ۲ }}
$$
محاسبه محیط بیضی با سری های بی نهایت
علاوه بر فرمولهای تقریبی، فرمولهای دیگری نیز وجود دارند که اصطلاحا با عنوان فرمولهای دقیق شناخته میشوند. این فرمولها، برای محاسبه محیط بیضی با دقت بالا، از مفهوم سریهای بینهایت بهره میگیرند. سری، مجموع جملات یک دنباله است. حاصلجمع دنبالهها میتواند همگرا یا واگرا باشد. سریهای همگرا، به یک عدد مشخص میل میکنند. سریهای معرفی شده در این بخش، با هر عبارت، به اندازه دقیق محیط بیضی نزدیکتر میشود.
فرمول ششم: سری بی نهایت با ثابت خروج از مرکز
یکی از شناخته شدهترین سریهای همگرا در مبحث محیط بیضیها، سری بینهایت زیر است:
$$
p=۲ a pileft( ۱ -sum_{ i = ۱ }^{infty} frac{( ۲ i ) !^{ ۲ }}{left( ۲^{ i } times i !right)^{ ۴ }} times frac{e^{ ۲ i}}{ ۲ i-1}right)
$$
به ثابت e در سری بالا، خروج از مرکز بیضی میگویند. این ثابت، کمیتی برای نمایش میزان فشردگی یا کشیدگی بیضی نسبت به دایره است. e، با استفاده از رابطه زیر محاسبه میشود:
$$
e = frac {sqrt { a^۲ – b^۲ }}{ a }
$$
اگر عبارتهای اول این سری را بنویسیم، فرم ریاضی آن به شکل زیر در میآید:
$$
p= ۲ a pileft[ ۱ -left(frac{ ۱ }{ ۲ }right)^{ ۲ } e^{ ۲ }-left(frac{۱ times ۳ }{ ۲ times ۴ }right)^{ ۲ } frac{e^{ ۴ }}{ ۳ }-left(frac{۱ times ۳ times ۵ }{ ۲ times ۴times ۶ }right)^{ ۲ } frac{e^{ ۶ }}{ ۵ }-ldotsright]
$$
همانطور که از عنوان سریهای بینهایت مشخص است؛ عبارتهای این سریها تا بینهایت ادامه مییابند. از اینرو، برای رسیدن به یک جواب قطعی، حل عبارتها را باید تا بینهایت ادامه داد. به عبارت دیگر، هر چه تعداد عبارتهای نوشته شده بیشتر باشد، جواب به دست آمده دقیقتر خواهد بود.
فرمول هفتم: سری بی نهایت با ثابت h
از دیگر سریهای بینهایت محبوب در مبحث محاسبه محیط بیضی، میتوان به سری زیر اشاره کرد:
$$
p=pi(a+b) sum_{n=۰}^{infty}left(begin{array}{c}
۰/۵
n
end{array}right)^{۲} h^{n}
$$
ثابت h، همان ثابت مورد استفاده در تقریبهای رامانوجان است:
$$
h=frac{(a-b)^{۲}}{(a+b)^{۲}}
$$
حل سری بالا، در نگاه اول کمی پیچیده به نظر میرسد. با این وجود، اگر برخی از عبارتهای اول آن را بنویسیم، به رابطه نسبتا ساده زیر میرسیم:
$$
p=pi ( a + b )left(۱ + frac{ ۱ }{ ۴ } h+frac{ ۱ }{ ۶۴ } h^{ ۲ }+frac{ ۱ }{ ۲۵۶ } h^{ ۳ }+ldotsright)
$$
در اینجا نیز مانند سری قبلی، هر چه عبارتهای بیشتری را به محاسبات خود اضافه کنیم، عدد به دست آمده برای محیط دقیقتر میشود. تفاوت اصلی این سری با سری قبلی این است که با نوشتن عبارتهای کمتر میتوان به یک جواب بسیار دقیق رسید.
محاسبه محیط بیضی با انتگرال
دقیقترین روش محاسبه محیط بیضی، استفاده از معادلات انتگرالی است. در ادامه، به معرفی فرمولهای انتگرالی محیط بیضیها میپردازیم.
فرمول هشتم: رابطه دقیق محیط با خروج از مرکز
تابع زیر، کاملترین فرمول محیط بیضی است:
$$
P=۴ int_{ ۰ }^{a} sqrt{ ۱ +frac{b^{ ۲ } x^{ ۲ }}{a^{ ۲ }left(a^{ ۲ }-x^{ ۲ }right)}} d x
$$
در صورت نوشتن معادله پارامتری این تابع، به رابطه زیر میرسیم:
$$
P = ۴ a int_{ ۰ }^{ pi / ۲ } sqrt{۱-e^{۲} sin ^{ ۲ } theta} d theta
$$
e، ثابت خروج از مرکز بیضی با رابطه زیر را نمایش میدهد:
$$
e = frac {sqrt {a^۲ – b^۲ }}{a}
$$
در صورت هماندازه بودن محورهای بزرگ و کوچک بیضی (حالت دایره)، e برابر با صفر میشود. به این ترتیب، جواب معادله برابر با 2πr خواهد شد. با وجود دقیق بودن رابطه انتگرالی محیط بیضی، رسیدن به جواب قطعی در آن، نیاز به نوشتن بینهایت عبارت دارد. به همین دلیل، معمولا از فرمولهای انتگرالی دیگر برای محاسبه محیط بیضی استفاده میشود.
فرمول نهم: طول کمان بیضی
طول یک کمان یک بیضی با تابع y=f(x) در بازه a تا b، برابر است با:
$$
L = int_{a}^{b} sqrt{۱+left(y^{prime}right)^{۲}} d x
$$
بر اساس رابطه بالا، به منظور تعیین طول کمان باید از مشتق تابع آن (‘y) در انتگرال استفاده کنیم. معادله بیضی به صورت زیر نوشته میشود:
$$
frac{x^{ ۲ }}{a^{ ۲ }}+frac{y^{ ۲ }}{b^{ ۲ }} = ۱$$
$$
y = pm frac{ b }{ a } sqrt{ a^{ ۲ } – x^{ ۲ }}
$$
مشتق y برابر است با:
$$
y’ = frac { -bx } { a sqrt {a^{ ۲ } – b^{ ۲ }} }
$$
برای نوشتن فرمول طول کمان بیضی، شکل زیر را در نظر بگیرید.
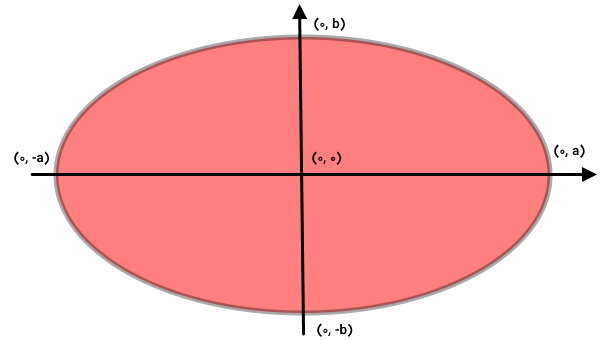
مرکز بیضی بالا، بر روی مبدا مختصات (۰ و ۰) قرار دارد. با محاسبه انتگرال در بازه 0 تا a (ربع اول)، طول کمانی به اندازه یکچهارم محیط بیضی به دست میآید. ‘y را درون فرمول انتگرالی محاسبه طول کمان در بازه 0 تا a قرار میدهیم:
$$
L=int_{ ۰ }^{ a } sqrt{ ۱+frac{ b^{ ۲ } x^{ ۲ }}{a^{ ۲ }left(a^{ ۲ }-x^{ ۲ }right)}} d x
$$
اگر رابطه بالا را در عدد 4 ضرب کنیم، به فرمول محاسبه محیط بیضیها میرسیم:
$$
P = ۴ int_{ ۰ }^{a} sqrt{ ۱+frac{b^{ ۲ } x^{ ۲ }}{a^{ ۲ }left(a^{ ۲ }-x^{ ۲ }right)}} d x
$$
فرمول دهم: معادلات پارامتریک طول کمان بیضی
شعاع بزرگ و کوچک بیضی، با a و b نمایش داده میشوند. معادلات پارامتریک بیضی عبارت هستند از:
$$
x = a cos { theta }
$$
$$
y = b cos { theta }
$$
طول کمانی با تابع ((θ)x(θ), y) در بازه [a, b] از رابطه زیر به دست میآید:
$$
int_{ a }^{ b }left( x^{prime}( theta )right)^{ ۲ } + left( y^{ prime }( theta )right )^{ ۲ } d t
$$
با قرار دادن معادلات پارامتریک بیضی درون انتگرال بالا و حل آن در بازه 0 تا π/2، محیط بیضی در ربع اول محاسبه میشود. بنابراین، به منظور تعیین محیط کل، باید انتگرال را در عدد 4 ضرب کنیم:
$$
begin{aligned}
P &= ۴ int_{ ۰ }^{pi / ۲} sqrt{( -a sin theta)^{ ۲ }+( b cos theta)^{۲}} d theta
&= ۴ int_{ ۰ }^{pi / ۲ } sqrt{ a^{ ۲ }left( ۱ -cos ^{ ۲ } thetaright)+b^{۲} cos ^{۲} theta} d theta
&= ۴ int_{ ۰ }^{pi / ۲ } sqrt{ a^{ ۲ }-left(a^{ 2 }-b^{ ۲ }right) cos ^{ ۲ } theta} d theta
&= ۴ a int_{ ۰ }^{pi / ۲ } sqrt{ ۱ – left( ۱ -frac{ b^{ ۲ }}{ a^{ ۲ }}right) cos ^{ ۲ } theta} d theta
&= ۴ a int_{ ۰ }^{pi / ۲ } sqrt{ 1 – e^{ ۲ } cos ^{ ۲ } theta} d theta
end{aligned}
$$
رابطه بالا را میتوانیم بر حسب سینوس نیز بازنویسی کنیم:
$$
P = ۴ a int_{ 0 }^{pi / ۲ } sqrt{ ۱ – e^{ ۲ } sin ^{ ۲ } theta} d theta
$$
محاسبه محیط شکلهای هندسی شناخته شده نظیر مربع، مستطیل، لوزی، دایره، متوازیالاضلاع و غیره، معمولا با استفاده از فرمولهای دقیق و در عین حال ساده انجام میگیرد. در طرف مقابل، محاسبه محیط بیضی، نسبتا پیچیده است و نیاز به اطلاعات کافی در زمینه مفاهیم پیشرفتهتر ریاضی دارد. در صورت علاقه به یادگیری این مفاهیم، مطالعه مقالههای موجود در «فهرست مطالب ریاضی مجله فرادرس» را به شما پیشنهاد میکنیم.
مقایسه محیط انواع بیضی
یکی از مهمترین نکات استفاده از فرمولهای مختلف محاسبه محیط بیضی، دقت یا خطای آنها است. این نکته، بر روی کاربرد هر فرمول در شرایط خاص تاثیر میگذارد. به عنوان مثال، در صورت وجود اختلاف اندازه زیاد بین محورهای اصلی و فرعی، استفاده از تقریب دایره مناسب نیست. در این شرایط، استفاده از تقریبهای دیگر یا فرمولهای رامانوجان، گزینه بهتری خواهد بود. تصویر متحرک زیر، خطای تقریبهای مختلف را با توجه به افزایش نسبت اندازه محور اصلی به محور فرعی نمایش میدهد.
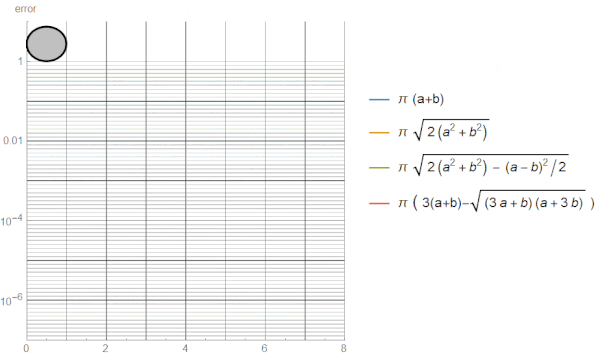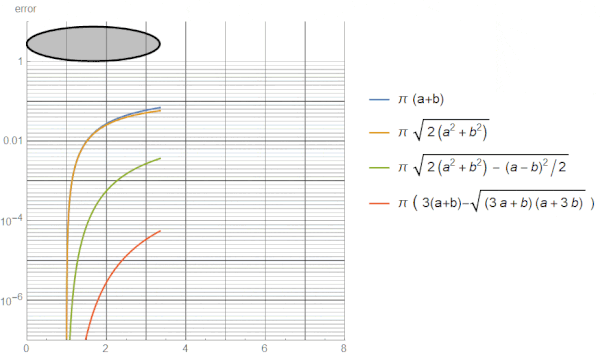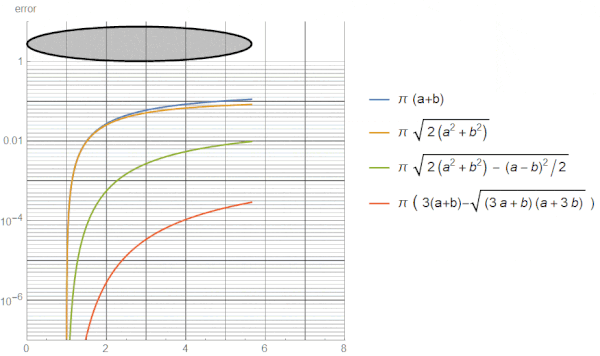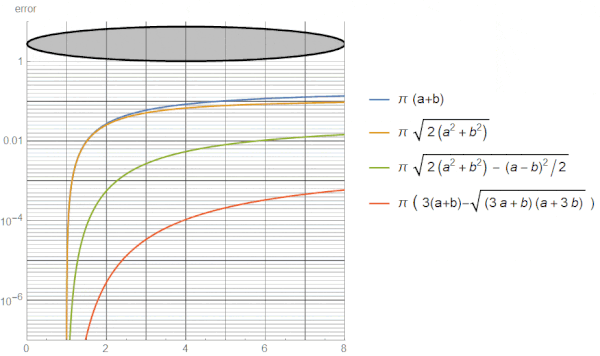
همانطور که مشاهده میکنید، در صورت افزایش نسبت محور اصلی به فرعی، خطای دو تقریب اول به بیش از 10 درصد میرسد. این خطا شاید برای اندازههای کوچک ناچیز به نظر برسد؛ اما در اندازههای بزرگ، مقدار عددی خطا، قابل توجه و بسیار تاثیرگذار خواهد بود. در طرف مقابل، دقت محاسباتی دو تقریب دیگر، مناسب است. خطای یکی از این تقریبها به حدود 3 درصد و خطای تقریب دیگر به زیر 1 صدم درصد میرسد.
مقایسه نتایج به دست آمده از فرمولهای محاسبه محیط بیضی در حالتهای خاص نیز میتواند درک خوبی را از کاربرد و دقت هر یک از گزینههای موجود فراهم کند. دایره و خط را میتوان به عنوان دو حالت خاص برای انجام این مقایسه در نظر گرفت. اگر شعاع بزرگ و کوچک یک بیضی برابر باشد (a=b)، جواب تمام تقریبها، یکسان خواهد بود. در صورتی که اندازه یکی از شعاعها به صفر میل کند (a=0 یا b=0)، محیط بیضی، برابر با شعاع غیر صفر میشود. جدول زیر، مقایسه نتایج حاصل از فرمولهای اول تا هفتم را برای دو حالت خاص بیضی نمایش میدهد.
| محیط بیضی با 10=a=b (دایره) | محیط بیضی با a=0 و b=10 (خط) | |
| فرمول اول | 62/8 | 31/4 |
| فرمول دوم | 62/8 | 44/4 |
| فرمول سوم | 62/8 | 47/1 |
| فرمول چهارم | 62/8 | 39/8 |
| فرمول پنجم | 62/8 | 39/8 |
| فرمول ششم | 62/8 | 42/9 |
| فرمول هفتم | 62/8 | 39/8 |
| جواب دقیق | 62/8 | 40 |
محاسبه محیط بیضی آنلاین
در بخشهای قبلی دیدیم که نوشتن فرمولهای محیط بیضی و به دست آوردن یک جواب دقیق با استفاده از این فرمولها، فرآیند نسبتا پیچیدهای دارد. این موضوع، خطای انسانی در انجام محاسبات را افزایش میدهد. ماشینحسابهای آنلاین محیط بیضی، ابزارهای مفید و ارزشمندی هستند که محاسبات مورد نظر را با دقت خوبی انجام میدهند. یکی از بهترین و سادهترین ابزارهای اینترنتی موجود برای محاسبه آنلاین محیط بیضی، موتور جستجوی گوگل (+) است. با جستجوی عبارتهایی نظیر «ellipse circumference» یا «ellipse perimeter» در گوگل، کادری مشابه تصویر زیر در ابتدای صفحه نتایج ظاهر میشود.
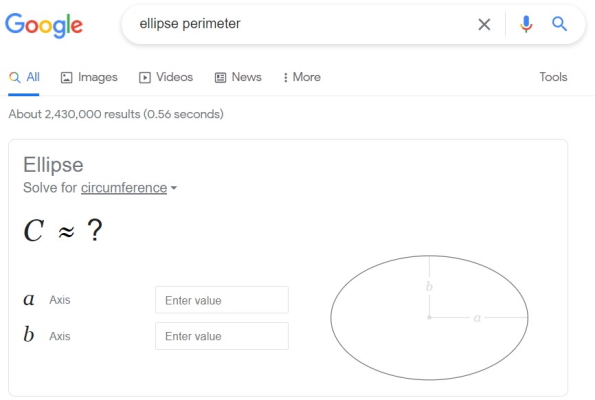
کار کردن با ماشین حساب گوگل بسیار ساده است. به منظور تعیین محیط بیضی، اندازه یکی از شعاعها را درون کادر «a Axis» و اندازه شعاع دیگر را درون کادر «b Axis» وارد میکنیم. به محض تایپ عدد دوم، محیط بیضی محاسبه میشود. مقدار عدد محیط در بالای کادر و روند محاسبات آن در پایین کادر به نمایش در میآید. به عنوان مثال، تصویر زیر، خروجی محیط یک بیضی با شعاع بزرگ 4 و شعاع کوچک 1 را نمایش میدهد.
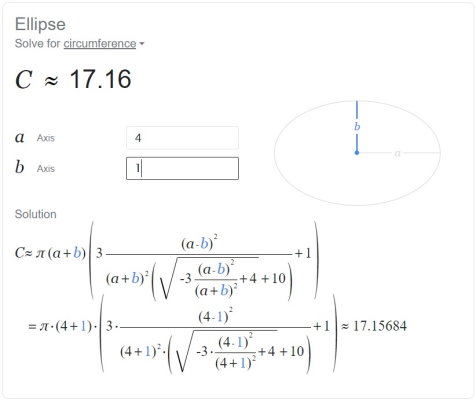
از دیگر گزینههای محاسبه آنلاین مساحت بیضی، میتوان به سایت Omni Calculator (+) و سایت Keisan (+) اشاره کرد. مبنای محاسباتی ابزارهای این دو سایت، مشابه با ماشین حساب گوگل هستند. البته به دلیل تخصصی بودن آنها، این سایتها، امکانات بیشتری را در اختیار کاربران قرار میدهند.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
برچسب : نویسنده : خنجی darsi بازدید : 1584
آرشیو مطالب
- مرداد 1392
- دی 1394
- بهمن 1394
- فروردين 1395
- ارديبهشت 1395
- خرداد 1395
- تير 1395
- بهمن 1396
- اسفند 1396
- شهريور 1396
- دی 1397
- بهمن 1397
- ارديبهشت 1397
- تير 1397
- آبان 1397
- آذر 1397
- دی 1398
- بهمن 1398
- اسفند 1398
- ارديبهشت 1398
- مرداد 1398
- مهر 1398
- آذر 1398
- دی 1399
- بهمن 1399
- اسفند 1399
- فروردين 1399
- خرداد 1399
- تير 1399
- مرداد 1399
- شهريور 1399
- مهر 1399
- بهمن 1400
- اسفند 1400
- فروردين 1400
- ارديبهشت 1400
- خرداد 1400
- تير 1400
- مرداد 1400
- دی 1401
- بهمن 1401
- اسفند 1401
- فروردين 1401
- ارديبهشت 1401
- خرداد 1401
- تير 1401
- مرداد 1401
- شهريور 1401
- مهر 1401
- آبان 1401
- آذر 1401
- دی 1402
- بهمن 1402
- اسفند 1402
- فروردين 1402
- ارديبهشت 1402
- خرداد 1402
- تير 1402
- مرداد 1402
- شهريور 1402
- مهر 1402
- آبان 1402
- آذر 1402
- فروردين 1403
- ارديبهشت 1403
