کدهای متلب محاسبات عددی | دانلود رایگان مجموعه کامل

در این مطلب روش‌ها و کدهای متلب محاسبات عددی را معرفی می‌کنیم. محاسبات عددی روش‌ها و ویژگی‌های متفاوتی دارند. در این مبحث ضمن معرفی این روش‌ها، کدها و حل دستی برخی از آن‌ها را معرفی می‌کنیم. اگر شما نیز برای حل مسائل ریاضی، مهندسی یا فیزیکی خود به حل عددی نیازمند هستید خواندن این مطلب را از دست ندهید.

محاسبات عددی در متلب

محاسبات عددی روشی برای حل مسائل پیچیده ریاضی است که فقط با استفاده از عملگرهای ساده ریاضی انجام می‌شود. این روش شامل فرمول‌بندی فیزیکی مدل‌های ریاضی و موقعیت‌هایی است که می‌توان با عملگرهای ریاضی حل کرد. برای محاسبات عددی نیاز به توسعه، تجزیه و تحلیل و استفاده از الگوریتم‌ها است. این محاسبات شامل تعداد زیادی محاسبات ریاضی هستند و بنابراین به دستگاه‌های محاسباتی سریع و کارآمد احتیاج دارند. انقلاب میکروالکترونیک و متعاقب آن توسعه رایانه‌های شخصی ارزان و کم هزینه تأثیر به سزایی در استفاده از روش‌های عددی برای حل مشکلات علمی داشته است. روش‌های معادلات عددی برای حل حالت‌های زیر اتفاق می‌افتد:

• معادلات غیر خطی تک متغیره که حل تحلیلی و بسته ندارند و برای آن‌ها باید از حل عددی استفاده کرد.
• روش درون‎‌یابی و برازش برای پیدا کردن معادلاتی که داده‌هایی از آن را داریم.
• حل عددی مشتق‌ها و انتگرال‌هایی که حل تحلیلی و دقیقی ندارند.
• حل عددی معادلات دیفرانسیل معمولی یا ODE
• حل عددی دستگاه معادلات خطی یا غیرخطی. البته حل تحلیلی دستگاه معادلات خطی غالباً امکان‌پذیر است اما در حالتی که تعداد متغیرها و معادلات زیاد باشند حل تحلیلی این معادلات زمان زیادی می‌گیرد و در این حالت بهتر است به حل عددی روی بیاوریم.
• حل عددی برای به دست آوردن ویژه مقادیر ماتریس‌ها.
• الگوریتم حداقل مربعات که مجموعه‌ای از داده‌ها را با یک تابع نمایی، هایپربولیک یا … فیت می‌کند و به این ترتیب اطلاعات بیشتری از یک سیستم به دست می‌آوریم.
• بهینه سازی عددی نیز برای بهینه کردن یک پارامتر در یک سیستم به کار می‌رود.

نکته‌ای که در محاسبات عددی مهم است میزان خطا در این محاسبات است که باید آن را نیز مد نظر قرار داد. در این مطلب چند روش محاسبه عددی در متلب را معرفی می‌کنیم و چند مثال از این روش‌ها را حل می‌کنیم.

حل عددی دستگاه معادلات خطی

در روش حل عددی دستگاه معادلات خطی می‌توان به روش‌های تکراری و غیرتکراری در نرم افزار متلب اشاره کرد که به گروه‌های زیر تقسیم‌بندی می‌شوند:

روش‌های غیرتکراری

• کدهای متلب محاسبات عددی و روش گاوس ناقص
• کدهای متلب محاسبات عددی و روش گاوس یا پیووتینگ
• کدهای متلب محاسبات عددی و روش تجزیه LU

روش‌های تکراری

• کدهای متلب محاسبات عددی و روش ژاکوبی
• کدهای متلب محاسبات عددی و روش گاوس-سیدال

در دستگاه معادلات خطی برای حل یک دستگاه باید تعداد ضرایب معلوم و مجهول با هم برابر باشند. برای حل این دستگاه‌ها ابتدا آن‌ها را به فرمت ماتریسی در می‌آوریم. در حقیقت دستگاه معادلات زیر را در نظر بگیرید:

$$begin{cases}a_{11}x_{1}+a_{12}x_{2}+cdots+a_{1n}x_{n}=b_{1} \ a_{21}x_{1}+a_{22}x_{2}+cdots+a_{2n}x_{n}=b_{2}\
vdots quad quad quad quadvdots quad quad quad quad quad quadvdots\
a_{m1}x_{1}+a_{m2}x_{2}+cdots+a_{mn}x_{n}=b_{m}
end{cases}$$

فرم ماتریسی این دستگاه را می‌توان به شکل خلاصه شده زیر نوشت:

$$Ax=b$$

که A، x و b به ترتیب ماتریس‌های $$mtimes n$$، $$1 times n$$ و $$1times m$$ هستند و به صورت زیر نمایش داده می‌شوند:

$$begin{bmatrix}
a_{11}& a_{12}&cdots & a_{1n}\
a_{21}&a_{22}&cdots & a_{2n}\
vdots & vdots & cdots & vdots\
a_{m1}&a_{m2}& cdots & a_{mn}
end{bmatrix}begin{bmatrix}
x_{1}\
x_{2}\
vdots\
x_{n}\
end{bmatrix}=begin{bmatrix}
b_{1}\
b_{2}\
vdots\
b_{m}\
end{bmatrix}$$

برای حل این دستگاه معادلات خطی همان طور که گفتیم می‎‌توان از روش‌های مستقیم و غیرمستقیم استفاده کرد. در روش‌های مستقیم پاسخ اعداد ثابتی هستند که این اعداد شامل خطاهای حاصل از گردکردن می‌باشند و در روش‌های غیرمستقیم اصل بر حدس‌های پی در پی برای پاسخ به مسئله طرح ریزی شده است. در بین روش‌های مستقیم یا غیرتکراری حل عددی دستگاه معادلات خطی می‌توان به روش‎‌های زیر اشاره کرد:

1. کدهای متلب محاسبات عددی و روش معکوس ماتریس ضرایب
2. کدهای متلب محاسبات عددی و روش کرامر
3. کدهای متلب محاسبات عددی و روش‌های حذفی که شامل روش ساده (ناقص) گاوس و روش گاوس است.
4. کدهای متلب محاسبات عددی و روش تجزیه

نکته مهم در استفاده از این روش‌ها که در بالا بیان شد غیرصفر بودن دترمینان ماتریس ضرایب یا ماتریس A که در بالا معرفی کردیم است. در اینجا به بررسی روش حذف ساده (ناقص) گاوس می‌پردازیم.

روش ساده (ناقص) گاوس

یکی از محدودیت‌های این روش این است که تنها در صورت غیر صفر بودن قطر اصلی ماتریس ضرایب این روش کاربرد دارد. در این روش باید یک ماتریس افزوده تشکیل دهیم که مجموع ماتریس ضرایب و ماتریس معلومات مسئله است. در ماتریس افزوده یک ستون به ماتریس ضرایب اضافه می‌شود که همان ماتریس معلومات مسئله است. برای درک این روش یک مثال را با این روش حل می‌کنیم و سپس آن را در متلب نیز اجرا خواهیم کرد.

فرض کنید چهار مجهول داریم که فرم ماتریسی آن به صورت زیر است:

$$begin{bmatrix}
1& 1&1 & 1\
2&3&1 & 5\
-1 & 1 & -5 & 3\
3&1&7 & -2\
end{bmatrix}begin{bmatrix}
x_{1}\
x_{2}\
x_{3}\
x_{4}\
end{bmatrix}=begin{bmatrix}
10\
31\
-2\
18\
end{bmatrix}$$

می‌خواهیم این دستگاه چهار معادله و چهار مجهول را با روش ساده گاوس حل کنیم. روش کار به این صورت است که اگر $$a_{kk}$$ مخالف صفر باشد آن گاه این روش کاربرد دارد و ضرایب جدیدی تحت عنوان m برای $$k$$اُمین سطر از ماتریس افزوده به صورت زیر تعریف می‌کنیم:

$$m_{ik}=frac{a_{ik}^{(k)}}{a_{lk}^{(k)}}Rightarrowbegin{cases}a_{ij}^{(k+l)}=a_{ij}^{(k)}-m_{ik}a_{kj}^{(k)}\ b_{i}^{(k+l)}=b_{i}^{(k)}-m_{ik}b_{k}^{(k)}end{cases}$$

حال به ترتیب سطر اول عنصر $$a_{11}$$ را که برابر با 1 است در نظر می‌گیریم و $$m_{21}$$ را محاسبه می‌کنیم که برابر است با:

$$m_{21}=frac{2}{1}=2$$

بدین ترتیب عناصر سطر دوم به صورت زیر تغییر می‌کنند:

$$begin{cases}a_{21}^{(2)}=a_{21}^{(1)}-m_{21}a_{11}=0 \ a_{22}^{(2)}=a_{22}^{(1)}-m_{21}a_{12}=1 \
a_{23}^{(2)}=a_{23}^{(1)}-m_{21}a_{13}=-1\
a_{24}^{(2)}=a_{24}^{(1)}-m_{21}a_{14}=3\
b_{2}^{(2)}=b_{2}^{(1)}-m_{21}b_{1}=11
end{cases}$$

همچنین برای سطر سوم $$m_{31}$$ برابر است با:

$$m_{31}=frac{-1}{1}=-1$$

و عناصر سطر سوم به شکل زیر درمی‌‌آیند:

$$begin{cases}a_{31}^{(2)}=a_{31}^{(1)}-m_{31}a_{11}=0 \ a_{32}^{(2)}=a_{32}^{(1)}-m_{31}a_{12}=2 \
a_{33}^{(2)}=a_{33}^{(1)}-m_{31}a_{13}=-4\
a_{24}^{(2)}=a_{24}^{(1)}-m_{31}a_{14}=4\
b_{3}^{(2)}=b_{3}^{(1)}-m_{31}b_{1}=8
end{cases}$$

و در نهایت در این مرحله برای سطر آخر $$m_{41}$$ برابر است با:

$$m_{41}=frac{3}{1}=3$$

و عناصر این سطر نیز به صورت زیر در می‌آیند:

$$begin{cases}a_{41}^{(2)}=a_{41}^{(1)}-m_{41}a_{11}=0 \ a_{42}^{(2)}=a_{42}^{(1)}-m_{41}a_{12}=-2 \
a_{43}^{(2)}=a_{43}^{(1)}-m_{41}a_{13}=4\
a_{44}^{(2)}=a_{44}^{(1)}-m_{41}a_{14}=-5\
b_{4}^{(2)}=b_{4}^{(1)}-m_{41}b_{1}=-12
end{cases}$$

بعد از انجام این مراحل ماتریس به شکل زیر در می‌آید و داریم:

$$begin{bmatrix}
1& 1&1 & 1&10\
0&1&-1 & 3&11\
0 & 2 & -4 & 4&8\
0&-2&4 & -5&-12\
end{bmatrix}$$

حالا همین مراحل را برای عنصر $$a_{22}$$ در نظر می‌گیریم و به سمت سطر‌های پایین یعنی سطرهای 3 و 4 حرکت می‌کنیم. در این حالت $$m_{32}$$ برابر است با:

$$m_{32}=frac{2}{1}=2$$

بدین ترتیب عناصر سطر سوم به صورت زیر تغییر می‌کنند:

$$begin{cases}a_{32}^{(3)}=a_{32}^{(2)}-m_{32}a_{22}=0 \ a_{33}^{(3)}=a_{33}^{(2)}-m_{32}a_{23}=-2 \
a_{34}^{(3)}=a_{34}^{(2)}-m_{32}a_{24}=-2\
b_{3}^{(3)}=b_{3}^{(2)}-m_{32}b_{2}=-14
end{cases}$$

همچنین عنصر $$m_{42}$$ برابر است با:

$$m_{42}=frac{-2}{1}=-2$$

و عناصر سطر چهارم به صورت زیر می‌شوند:

$$begin{cases}a_{42}^{(3)}=a_{42}^{(2)}-m_{42}a_{22}=0 \ a_{43}^{(3)}=a_{43}^{(2)}-m_{42}a_{23}=2 \
a_{44}^{(3)}=a_{44}^{(2)}-m_{42}a_{24}=1\
b_{4}^{(3)}=b_{4}^{(2)}-m_{42}b_{2}=10
end{cases}$$

و بدین ترتیب ماتریس افزوده به صورت زیر در می‌آید:

$$begin{bmatrix}
1& 1&1 & 1&10\
0&1&-1 & 3&11\
0 & 0 & -2 & -2&-14\
0&0&2 & 1&10\
end{bmatrix}$$

در مرحله بعد $$a_{33}$$ را در نظر می‌گیریم و $$m_{43}$$ را محاسبه می‌کنیم که برابر است با:

$$m_{43}=frac{2}{-2}=-1$$

حال عناصر سطر چهارم به شکل زیر تغییر می‌کنند و داریم:

$$begin{cases}a_{43}^{(4)}=a_{43}^{(3)}-m_{43}a_{33}=0 \ a_{44}^{(4)}=a_{44}^{(3)}-m_{43}a_{34}=-1 \
b_{4}^{(4)}=b_{4}^{(3)}-m_{43}b_{3}=-4
end{cases}$$

و ماتریس در نهایت به شکل زیر در می‌آید:

$$begin{bmatrix}
1& 1&1 & 1&10\
0&1&-1 & 3&11\
0 & 0 & -2 & -2&-14\
0&0&0 & -1&-4\
end{bmatrix}$$

اگر این معادلات را به شکل جبری بنویسیم داریم:

$$begin{aligned}
x_{I}+x_{2}+x_{3}+x_{4} &=10 \
x_{2}-x_{3}+3 x_{4} &=11 \
-2 x_{3}-2 x_{4} &=-14 \
-x_{4} &=-4
end{aligned}$$

که به راحتی مقادیر $$x_{3}$$، $$x_{2}$$، $$x_{1}$$ و $$x_{4}$$ قابل محاسبه است. همین روش را در متلب می‌توان به صورت زیر نوشت اگر ماتریس ضرایب و مقادیر را مانند مثال بالا به عنوان ورودی بدهیم هر دو حالت جواب‌های یکسانی را نشان می‌دهند.

function ngaussel(A,b)
n=length(b);
x=zeros(n,1);
fprintf('n');
disp('The augmented matrix is')
augm=[A b]
for k=1:n-1 for i=k+1:n m=A(i,k)/A(k,k); for j=k+1:n A(i,j)=A(i,j)-m*A(k,j); end A(i,k)=m; b(i)=b(i)-m*b(k); end
end
x(n)=b(n)/A(n,n);
for i=n-1:-1:1 S=b(i); for j=i+1:n S=S-A(i,j)*x(j); end x(i)=S/A(i,i);
end
%print the result
fprintf('n');
disp('The transformed upper triangular augmented matrix C is')
fprintf('n');
for i=1:n for j=1:n if(j<i)A(i,j)=0;end end
end
C=[A b]
fprintf('n');
disp('Back substitution gives the vector solution')
x

برای اجرای دستور گاوس در متلب کد بالا را در یک اسکریپت با نام تابع یعنی ngaussel ذخیره کنید و در صفحه کار متلب ماتریس‌های A و b را تعریف کنید. با فراخوانی تابع این روش برای ماتریس ورودی شما اجرا شده و جواب نمایش داده می‌شود.

برای آشنایی بیشتر با محاسبات عددی در متلب، می‌توانید فیلم آموزش محاسبات عددی با MATLAB را مشاهده کنید که توسط فرادرس ارائه شده، لینک این آموزش در ادامه آورده شده است.

• برای دیدن فیلم آموزش محاسبات عددی با MATLAB + اینجا کلیک کنید.

درون‌یابی و برازش

درون‌یابی و برازش برای پیدا کردن صورت کلی توابعی است که داده‌هایی از آن را داریم. این داده‌ها می‌توانند از آزمایش یا مشاهده به دست آمده باشند. در حقیقت n زوج داده داریم که به صورت $$(x_{i}, y_{i})$$ هستند و می‌خواهیم $$y(x)$$ را تخمین بزنیم.

این روش در حل عددی بسیار متداول و رایج است و باید دقت کرد که این درون‌یابی با عبور از منحنی یا Curve fitting متفاوت است. در حقیقت در روش عبور از منحنی، منحنی که از بیشترین داده‌ها عبور می‌کند در نظر گرفته می‌شود اما در درون یابی باید تابع به دست آمده شامل تمام نقاط و داده‌ها باشد. انواع روش‌های درون یابی و برازش را می‌توان به صورت زیر دسته‌بندی کرد:

• کدهای متلب محاسبات عددی و روش لاگرانژ
• کدهای متلب محاسبات عددی و روش تفاضل‌های تقسیم شونده پیشرونده نیوتن
• کدهای متلب محاسبات عددی و اسپلاین‌های مرتبه دو و سه
• کدهای متلب محاسبات عددی و برازش یا عبور از منحنی

در ادامه این مطلب با حل یک مثال روش لاگرانژ را توضیح می‌دهیم.

درون یابی به روش لاگرانژ

با حل یک مثال روش لاگرانژ را توضیح می‌دهیم. در این مثال می‌خواهیم برای نقاط $${(0,6), (1,0), (2,2)} چند جمله‌ای مناسب را پیدا کنیم. برای به دست آوردن چند جمله‌ای مورد نظر آن را به صورت زیر معرفی می‌کنیم:

$$f(x)=sum_{i=0}^{n} L_{k}(x) y_{k}$$

ضرایب $$L_{k}(x)$$ به صورت زیر تعریف می‌شوند:

$$L_{k}(x)=frac{left(x-x_{0}right) cdotsleft(x-x_{k-1}right)left(x-x_{k+1}right) cdotsleft(x-x_{n}right)}{left(x_{k}-x_{0}right) cdotsleft(x_{k}-x_{k-1}right)left(x_{k}-x_{k+1}right) cdotsleft(x_{k}-x_{n}right)}=prod_{j=0 atop j=2}^{n} frac{x-x_{i}}{x_{k}-x_{i}}, k=0,1, cdots, n$$

به این ترتیب برای داده‌های مثال فوق ضرایب $$L_{k}(x)$$ برابر با روابط زیر به دست می‌آیند:

$$L_{0}(x)=frac{(x-1)(x-2)}{(0-1)(0-2)}=frac{x^{2}-3 x+2}{+2}$$

$$L_{1}(x)=frac{(x-0)(x-2)}{(1-0)(1-2)}=frac{x^{2}-2 x}{-1}$$

$$L_{2}(x)=frac{(x-0)(x-1)}{(2-0)(2-1)}=frac{x^{2}-x}{2}$$

بدین ترتیب داریم:

$$left{begin{array}{l}
f(x)=sum_{k=0}^{2} L_{k}(x) y_{k}=L_{2}(x) y_{0}+L_{1}(x) y_{1}+L_{2}(x) y_{2} \
f(x)=sum_{k=0}^{2} L_{k}(x) y_{k}=6 timesleft(frac{x^{2}-3 x+2}{2}right)+0 timesleft(frac{x^{2}-2 x}{-1}right)+2 timesleft(frac{x^{2}-x}{2}right) \
f(x)=4 x^{2}-10 x+6
end{array}right.$$

روش لاگرانژ در متلب به صورت زیر تعریف می‌شود:

function lagrange(x,y,a)
n=length(x);
p=0;
for k=1:n b(k)=1; d(k)=1; for j=1:n if j~=k b(k)=b(k)*(x(k)-x(j)); d(k)=d(k)*(a-x(j)); end end c(k)=y(k)/b(k); p=p+c(k)*d(k);
end
fprintf('n p(a)=%10.6f',p)
fprintf('n')

با تعریف بردارهای x ،y و مقدار a تابع به روش لاگرانژ محاسبه می‌شود و مقدار تابع به ازای a در خروجی چاپ می‌شود.

مشتق و انتگرال‌گیری عددی

مشتق و انتگرال‌گیری عددی زمانی مورد استفاده قرار می‌گیرد که تابع در دسترس نباشد و یا با یک تابع پیچیده رو به رو باشیم. روش‌های مشتق گیری عددی شامل موارد زیر هستند:

• بسط تیلور
• فرمول ریچاردسون

روش‌های انتگرال گیری عددی نیز به موارد زیر تقسیم می‌شوند:

• روش نیوتن-کوتز
• روش مجموع ریمان
• روش قاعده ذوزنقه‌ای
• روش سیمپسون
• الگوریتم رومبرگ

در ادامه این مطلب روش بسط تیلور را مورد معرفی و بررسی قرار می‌دهیم.

بسط تیلور

در ابتدا بسط تیلور توابع $$f(x+h)$$ را حول $$h=0$$ بررسی می‌کنیم و داریم:

$$begin{array}{l}
f(x+h)=f(x)+h f^{prime}(x)+frac{1}{2 !} h^{2} f^{prime prime}(x)+frac{1}{3 !} h^{3} f^{prime prime}(x)+cdots \
Rightarrow frac{f(x+h)-f(x)}{h}=f^{prime}(x)+left[frac{1}{2 !} h f^{prime prime}(x)right]+frac{1}{3 !} h^{2} f^{prime prime}(x)+cdots
end{array}$$

همین بسط برای تابعی به صورت $$f(x-h)$$ حول $$h=0$$ به صورت زیر است:

$$begin{array}{l}
f(x-h)=f(x)-h f^{prime}(x)+frac{1}{2 !} h^{2} f^{prime prime}(x)-frac{1}{3 !} h^{3} f^{prime prime}(x)+cdots \
Rightarrow frac{f(x)-f(x-h)}{h}=f^{prime}(x)-left[frac{1}{2 !} h f^{prime prime}(x)right]+frac{1}{3 !} h^{2} f^{prime prime}(x)-cdots
end{array}$$

اگر دو رابطه بالا را با یکدیگر جمع کنیم جوابی به صورت زیر خواهیم داشت:

$$frac{f(x+h)-f(x-h)}{2 h}=f^{prime}(x)+frac{1}{3 !} h^{2} f^{prime prime}(x)-cdots$$end{array}$$

بدین ترتیب می‌توان فرمول‌های تقریبی برای مشتق گیری مرتبه اول را به فرم‌های زیر تعریف کرد:

• تقریب اختلاف پیشرونده که به صورت زیر تعریف می‌شود:

$$f^prime(x)approx frac{f(x+h)-f(x)}{h}$$

• همچنین تقریب اختلاف پسرو به شکل زیر است:

$$f^prime(x)approx frac{f(x)-f(x-h)}{h}$$

• و تقریب اختلاف مرکزی نیز شکل زیر را می‌گیرد:

$$f^prime(x)approx frac{f(x+h)-f(x-h)}{2h}$$

با محاسبات می‌توان دید که با توجه به این که $$h$$ همواره مقداری کوچکتر از یک دارد، خطای محاسباتی در روش مشتق گیری مرکزی از دو روش پیشرو و پسرو کمتر خواهد بود. همچنین مشتق دوم تابع $$f(x)$$ با توجه به روش مشتق گیری مرکزی حول نقطه $$h=0$$ به شکل زیر خواهد بود:

$$f^{primeprime}(x)approx frac{f(x+h)-2f(x)+f(x-h)}{h^{2}}$$

این روش را با یک مثال توضیح داده و آن را در متلب اجرا می‌کنیم. برای تابع $$f(x)=sin(x)$$ مقدار تخمینی مشتق دوم آن را به ازای مقدار $$x=0.8quad rad$$ و $$h=0.01$$ محاسبه کنید و خطای محاسبات را به دست آورید.

با استفاده از رابطه مشتق دوم از روش بسط تیلور مقدار تخمینی مشتق برابر با $$-0.6967009$$ خواهد شد. این در حالی است که مقدار واقعی از روابط تحلیلی مقداری برابر با $$-0.6967067$$ دارد. به این ترتیب مقدار خطا برابر با $$5.81e-6$$ خواهد بود.

این مثال را در متلب به صورت زیر می‌نویسیم:

clear all
h=0.01;
t=(0:h:1);
a=sin(2*pi*1*t);
d2a=-((2*pi*1)^2)*sin(2*pi*1*t);
d2f=diff(a,2)/(h*h);
subplot(211),plot(t,d2a,'b',t(3:end),d2f,'r');
subplot(212), plot(t(3:end),abs(d2a(3:end)-d2f));
err=norm(d2f-d2a(3:end),2)/norm(d2a(3:end),2)

با اجرای این برنامه نمودارها به صورت زیر نمایش داده می‌شوند:

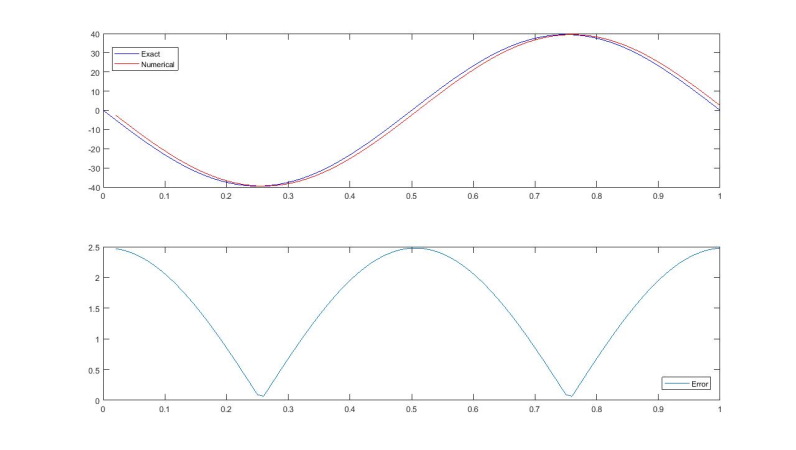
همچنین میزان ارور یا خطا نیز برابر با $$0.0622$$ در خروجی چاپ می‌شود.

حل عددی معادلات دیفرانسیل معمولی

در این بخش حل عددی معادلات دیفرانسیل معمولی را بررسی و معرفی می‌کنیم. به صورت کلی روش‌های حل عددی معادلات دیفرانسیل معمولی به صورت زیر معرفی می‌شوند:

• کدهای متلب محاسبات عددی و روش اویلر (بسط تیلور مرتبه اول)
• کدهای متلب محاسبات عددی و بسط‌های تیلور مرتبه‌های بالاتر از 1
• کدهای متلب محاسبات عددی و روش نقطه میانی
• کدهای متلب محاسبات عددی و روش رانگ-کوتای مرتبه 2 و 4
• کدهای متلب محاسبات عددی و روش آدامز-باشفورث
• کدهای متلب محاسبات عددی و روش آدامز-مولتون

در ادامه روش اویلر را معرفی کرده و با استفاده از یک مثال و بررسی آن به صورت دستی و در متلب این روش را توضیح می‌دهیم.

روش اویلر

ساده‌ترین شیوه تحلیلی از میان همه روش‌های محاسباتی در حل معادلات دیفرانسیل معمولی روش اویلر است. معادله‌ای مانند زیر را در نظر بگیرید که مقدار اولیه آن برابر با $$y(a)=y_{0}$$ است و در بازه تقریبی $$[a,b]$$ تعریف می‌شود و داریم:

$$frac{dy}{dt}=f(t,y)$$

برای شروع از روش اویلر ابتدا بازه را به $$N$$ زیر بازه مساوی تقسیم کرده و نقاط شبکه‌ای به صورت $$t_{i}=a+ih$$ به ازای $$i=0,1,2,…,N$$ تعریف می‌کنیم که $$h$$ یا گام حرکت برابر با $$h=frac{b-a}{N}$$ است. به این ترتیب بسط تیلور تابع $$y(t)$$ را حول $$t_{i}$$ می‌نویسیم و داریم:

$$y(t_{i+1})=y(t_{i}+h)=y(t_{i})+hy^{prime}(t_{i})+frac{h^{2}}{2}y^{primeprime}(zeta)$$

که $$zeta$$ مقداری بین $$t_{i}$$ و $$t_{i}+h$$ دارد. با صرف نظر از جملات دوم به بعد داریم:

$$yleft(t_{i}+hright) approx yleft(t_{i}right)+h y^{prime}left(t_{i}right)=y(t_{i})+hf(t_{i},y(t_{i}))$$

و با نمایش $$y(t_{i})$$ به صورت $$y_{i}$$ معادله به صورت زیر در می‌آید:

$$y_{i+1}=y_{i}+hf(t_{i},y_{i})quadquad i=0,1,cdots,N$$

معادله فوق به نام روش اویلر مشهور است. برای درک بیشتر موضوع مثال زیر را حل می‌کنیم و داریم:

$$y^{prime}=-6y$$

می‌دانیم که جواب این معادله دیفرانسیل برابر با $$y=exp(-6x)$$ است. بر اساس معادله اویلر داریم:

$$y_{i+1}=y_{i}+h(-6y_{i})$$

با نوشتن این تابع در متلب و برای گام‌هایی به طول $$0.1$$ و 10 گام و شرط اولیه $$y(1)=1$$ داریم:

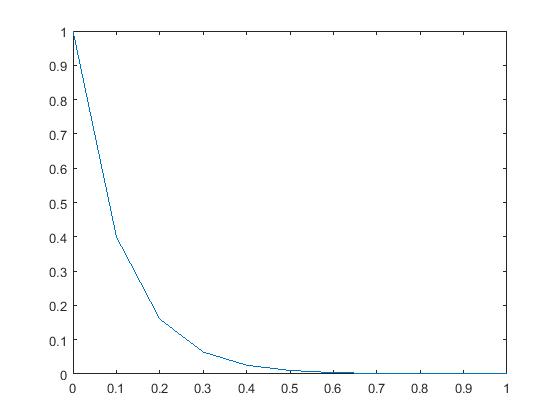
h=0.1; % step's size
N=10; % number of steps
y(1)=1;
for n=1:N
y(n+1)= y(n)+h*(-6*y(n));
x(n+1)=n*h;
end
plot(x,y)

با اجرای این مثال نموداری به شکل زیر در خروجی ظاهر می‌شود:

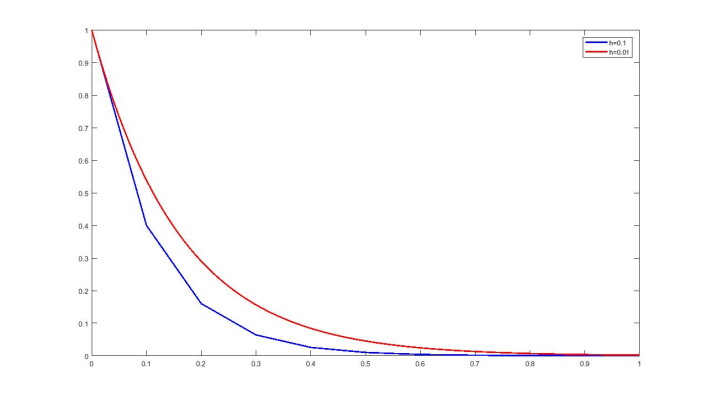
با تغییر طول گام و تعداد گام‌ها شکل نمودار به حالت منحنی یا curve نزدیکتر می‌شود و در این حالت خروجی به شکل زیر نمایش داده می‌شود:

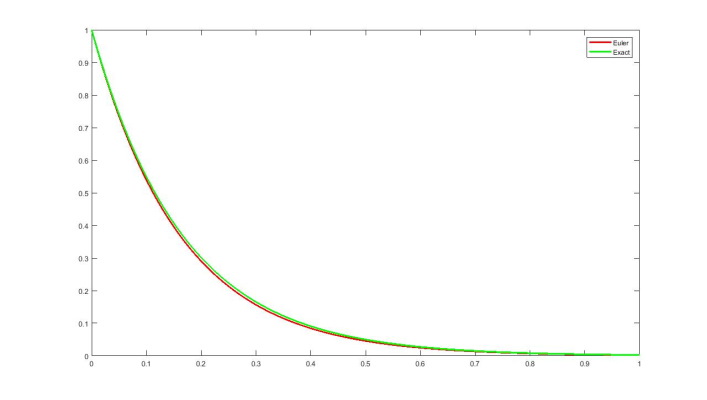
حال اگر حل عددی اویلر را با مشتق مستقیم تابع در همان بازه رسم کنیم و با یکدیگر مقایسه کنیم نتایج به صورت زیر نمایش داده می‌شوند:

h1=0.01; % step's size
N1=100; % number of steps
y(1)=1;
for n=1:N1
y(n+1)= y(n)+h1*(-6*y(n));
x(n+1)=n*h1;
end
plot(x,y,'r')
hold on
x=0:0.001:1;
y=exp(-6.*x);
plot(x,y,'g'

حل عددی معادلات دیفرانسیل غیرخطی

معادلات دیفرانسیل آهنگ تغییرات یک کمیت را نمایش می‌دهند. در مطلب حل دستگاه معادلات دیفرانسیل غیر خطی در متلب | گام به گام در مورد حل تحلیلی این معادلات در متلب صحبت کردیم در این بخش از این مبحث حل عددی معادلات دیفرانسیل غیرخطی در متلب را بررسی و معرفی می‌کنیم.

به صورت کلی معادلات دیفرانسیل ترکیبی از توابع و مشتقات آن‌ها هستند و بسیاری از مسائل فیزیکی و مهندسی را مدل‌سازی می‌کنند. این معادلات شامل شرایط اولیه یا شرایط مرزی هستند که با توجه با این شرایط این مسائل و معادلات مورد بررسی قرار می‌گیرند. انواع روش‌های عددی معادلات دیفرانسیل غیر خطی به سه دسته کلی تقسیم می‌شوند:

1. روش‌های ریشه یابی عددی دامنه محدود یا بسته
2. روش‌های ریشه یابی عددی دامنه نامحدود یا باز
3. حل عددی دستگاه معادلات غیرخطی به روش نیوتن

روش‌های ریشه یابی عددی دامنه محدود یا بسته را به دو روش نصف کردن یا Bisection و روش نابجایی یا موقعیت خطا می‌توان انجام داد. همچنین روش‌های ریشه یابی عددی دامنه نامحدود یا باز نیز به سه روش سکانت، نیوتون-رافسون و نقطه ثابت صورت می‌گیرد. در ادامه این بخش روش نصف کردن یا Bisection را معرفی می‌کنیم و آن را با حل یک مثال و بررسی آن در متلب توضیح خواهیم داد.

روش نصف کردن یا Bisection

روش نصف کردن برای هر تابع پیوسته‌ای مورد استفاده قرار می‌گیرد. برای استفاده از این روش باید تابع را در بازه‌ای در نظر بگیریم که ضرب مقادیر تابع در آن بازه کوچکتر از صفر و مشتق تابع مخالف صفر باشد. بدین ترتیب بازه تابع را نصف کرده و مقدار تابع را در آن نقطه به دست می‌آوریم و با توجه به شرایط آن را جایگزین مقدار اولیه یا نهایی بازه می‌کنیم یعنی داریم:

$$y=f(x)quad [a,b]$$
$$c=frac{(a+b)}{2}$$
$$begin{cases}ifquad f(a).f(c)<0rightarrow b=c\ if quad f(b).f(c)<0 rightarrow a=cend{cases}$$

این کار را تا جایی ادامه می‌دهیم تا مقدار $$f(c)$$ به صفر نزدیک شود. این روش را برای پیدا کردن ریشه تابع $$x^2-3$$ در بازه $$[1,2]$$ استفاده می‌کنیم. بدین ترتیب داریم:

function c = bisectionMethod(f,a,b,error)%f=@(x)x^2-3; a=1; b=2; (ensure change of sign between a and b) error=1e-4
c=(a+b)/2;
while abs(f(c))>error
if f(c)<0&&f(a)<0
a=c;
else
b=c;
end
c=(a+b)/2;
end

با تعریف تابع و بازه آن و دقت نزدیک بودن جواب به صفر و اجرای این کد ریشه این تابع در خروجی نمایش داده می‌شود.

معرفی فیلم آموزش محاسبات عددی با MATLAB

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آآموزش محاسبات عددی با MATLAB کرده است. این مجموعه آموزشی از شش درس تشکیل شده و برای دانشجویان رشته علوم پایه و فنی مهندسی مفید است. پیش‌نیاز این درس آموزش برنامه نویسی متلب (MATLAB) است.

درس اول این مجموعه به خطاها و اشتباهات در محاسبات عددی اختصاص دارد. درس دوم شامل حل دستگاه‌های معادلات خطی به روش محاسبات عددی در متلب است. درس سوم به درون‌یابی و برازش در متلب می‌پردازد و درس چهارم به مشتق گیری و انتگرال گیری عددی در متلب اختصاص دارد. در درس پنجم در مورد حل عددی معادلات دیفرانسیل معمولی در متلب خواهید آموخت. در نهایت در درس ششم ریشه یابی عددی معادلات غیرخطی در متلب به روش عددی آموزش داده می‌شود.

• برای دیدن فیلم آموزش محاسبات عددی با MATLAB + اینجا کلیک کنید.

جمع بندی

این مطلب به محاسبات عددی در متلب اختصاص داده شده است. در حقیقت روش‌ها و کدهای متلب محاسبات عددی بسیار گسترده هستند و روش‌های متفاوتی برای آن‌ها وجود دارد. در این مطلب این روش‌ها را به صورت فهرست وار معرفی کردیم و از هر کاربرد آن یک نمونه را با مثال و بررسی مثال در متلب توضیح دادیم.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های محاسبات عددی
• آموزش محاسبات عددی با MATLAB
• مجموعه آموزش‌های ریاضیات
• رسم تابع در متلب — آموزش گام به گام + نمونه کد
• حل معادله درجه ۲ در متلب | گام به گام (+ دانلود نمونه کد)
• دستور Sparse در متلب | به زبان ساده

نوشته کدهای متلب محاسبات عددی | دانلود رایگان مجموعه کامل اولین بار در مجله فرادرس. پدیدار شد.